那么在递归调用的时候,压栈压入的到底是什么了 对于阶乘来讲, into stack 就是那个int值吗 在研究bubble的时候出现了 Stackoverflow 那么是这种情况 into stack的又是什么
在Java中递归调用方法的时候,如果处理不好可能会出现Stackoverflow,也就是方法调用压栈最终超过栈空间分配的大小导致异常。在Scala中提供了尾递归优化,可以在一定程度上避免这种情况。以在阶乘中的应用为例。
import scala.annotation.tailrec
// 没有使用尾递归
def fac(n: Int): Int = {
if (n <= 1) n
else n * fac(n - 1)
}
// 使用尾递归
def fac(n: Int) = {
@tailrec def go(n: Int, acc: Int): Int = {
if (n <=0 ) acc
// 尾递归,顾名思义方法的调用也必须出现在返回值的位置
else go(n-1, acc * n)
}
go(n, 1)
}
接下来,将从两个方面来阐述这个问题:
(1) 函数调用流程
针对非尾递归调用,解释器必须要维护一个将要执行的操作的轨迹(下图的黑线), 递归操作一般是碰到指定条件才会停止压栈,如上面的n <= 0。
该链条的长度随N的增加而增加,所以称之为线性递归。它的运算过程是一个先扩展后收缩的过程,如下图所示。
如果程序中断了,要恢复的话还需要一些隐含的信息(比如说要恢复fac(2),就必须知道fac(1)的值),它们并没有保存在程序变量中,而是由解释器维持的运算所形成的链条,这个链条越长,需要保存的信息也就越多。

针对尾递归调用,每一次计算只需要维护当前的乘积, 计数器(n), 最大的N值。 这种过程叫做线性迭代过程, 并且计算轨迹不会像线性递归那样呈现先展开而后收缩的过程。
fac(6)
go(6, 1)
go(5, 1 * 6)
go(4, 1 * 6 * 5)
go(3, 1 * 6 * 5 * 4)
go(2, 1 * 6 * 5 * 4 * 3)
go(1, 1 * 6 * 5 * 4 * 3 * 2)
迭代过程就是那种其状态可以用固定数目的状态变量描述的计算过程,并且有一种规则描述着计算过程在从一个状态到下一状态转换时,这些变量的更新方式(本例中的乘),最后还有一个结束检测(递归调用的出口)。
如果上述过程在两个步骤之间停下来了,要想重新唤醒这一计算,只需要为解释器提供三个相关的变量即可。
It will execute an iterative process in constant space, even if the iterative process is described by a recursive procedure. An implementation with this property is called tail-recursive
关于占用的空间恒定实际上也是比较好理解的,线性递归每调用一次,链条长度会越长,会占用更大的空间。而线性迭代每一次调用只会依赖三个变量。
Scala中尾递归有如下两个限制: Scala只能针对调用同一函数的调用进行尾递归优化;递归的方法必须处于返回值的地方,才能使用尾递归优化。
(2) 函数调用过程中的栈
每一个函数(方法)在执行的时候都会创建一个栈帧来存储局部变量,操作数栈等。栈帧从入虚拟机栈到出虚拟机栈也对应着一个方法的执行完成。
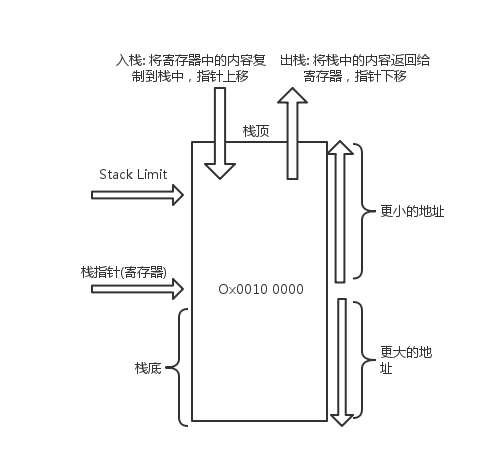
The stack pointer is usually a register that contains the top of the stack.
-
栈指针(Stack Pointer)实际上是一个寄存器(Register),包含着一个内存地址如0x0000 1000; 栈中比该值大的就是有效的; 比该值小的就是无效的(将会被GC的),所以随着入栈和出栈,栈指针会上下移动。但栈的大小是有限制的(Stack Limit), 也就是当栈指针向栈顶移动的时,如果对应位置的地址小于Stack Limit处的,则会导致StackOverflow。
-
压栈实际上就是将寄存器中的内容复制到栈中,然后栈指针上移; 出栈实际上就是将栈中的内容返回给寄存器,然后栈指针下移,之前的地址对应的空间变成无效。
-
在递归函数调用中,只有达到”出口”之后,调用才会一级一级的返回(也就是不断出栈,栈指针向栈底移动)。如果调用的栈太深,迟迟无法到达”出口”,就有可能导致栈指针超过Stack Limit。从而导致StackOverflow。
参考
> 计算机程序的构造与解释第一章
> 尾递归优化